17070번: 파이프 옮기기 1
유현이가 새 집으로 이사했다. 새 집의 크기는 N×N의 격자판으로 나타낼 수 있고, 1×1크기의 정사각형 칸으로 나누어져 있다. 각각의 칸은 (r, c)로 나타낼 수 있다. 여기서 r은 행의 번호, c는 열의
www.acmicpc.net
📝 문제
유현이가 새 집으로 이사했다. 새 집의 크기는 N×N의 격자판으로 나타낼 수 있고, 1×1크기의 정사각형 칸으로 나누어져 있다. 각각의 칸은 (r, c)로 나타낼 수 있다. 여기서 r은 행의 번호, c는 열의 번호이고, 행과 열의 번호는 1부터 시작한다. 각각의 칸은 빈 칸이거나 벽이다.
오늘은 집 수리를 위해서 파이프 하나를 옮기려고 한다. 파이프는 아래와 같은 형태이고, 2개의 연속된 칸을 차지하는 크기이다.
파이프는 회전시킬 수 있으며, 아래와 같이 3가지 방향이 가능하다.
파이프는 매우 무겁기 때문에, 유현이는 파이프를 밀어서 이동시키려고 한다. 벽에는 새로운 벽지를 발랐기 때문에, 파이프가 벽을 긁으면 안 된다. 즉, 파이프는 항상 빈 칸만 차지해야 한다.
파이프를 밀 수 있는 방향은 총 3가지가 있으며, →, ↘, ↓ 방향이다. 파이프는 밀면서 회전시킬 수 있다. 회전은 45도만 회전시킬 수 있으며, 미는 방향은 오른쪽, 아래, 또는 오른쪽 아래 대각선 방향이어야 한다.
파이프가 가로로 놓여진 경우에 가능한 이동 방법은 총 2가지, 세로로 놓여진 경우에는 2가지, 대각선 방향으로 놓여진 경우에는 3가지가 있다.
아래 그림은 파이프가 놓여진 방향에 따라서 이동할 수 있는 방법을 모두 나타낸 것이고, 꼭 빈 칸이어야 하는 곳은 색으로 표시되어져 있다.

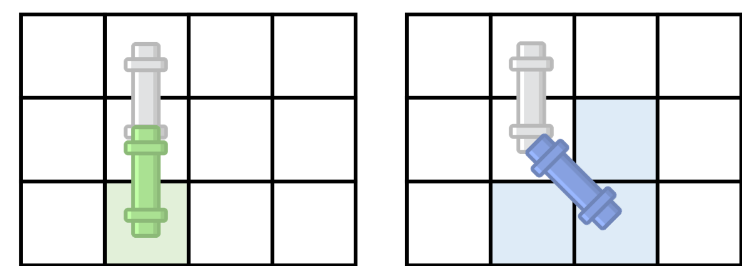

가장 처음에 파이프는 (1, 1)와 (1, 2)를 차지하고 있고, 방향은 가로이다. 파이프의 한쪽 끝을 (N, N)로 이동시키는 방법의 개수를 구해보자.
📜 풀이
- 경로 탐색 알고리즘에 기초하여 풀이할 수 있으나, 그럴 경우 Python3로 제출했을 때 시간초과가 발생한다.(Pypy3로 제출할 경우 통과함)
- 따라서 이를 DP를 사용하는 방법으로 구현하였다.
- 접근 방법은 다음과 같다.
- 특정 위치 (y, x)로 이동했을 때의 파이프의 방향은 가로, 세로, 대각선으로 총 세 종류가 된다.
- 즉, 특정 위치 (y, x)에 도착하는 경우의 수는 (파이프가 가로 방향인 상태로 도착하는 경우의 수) + (파이프가 세로 방향인 상태로 도착하는 경우의 수) + (파이프가 대각선 방향인 상태로 도착하는 경우의 수)일 것이다.
- 그렇다면 각각의 경우의 수는 어떻게 구할 수 있을까?
- 문제에 제시된 조건에 따라 경우의 수를 따져보면 다음과 같다.
- 파이프가 가로 방향인 상태로 특정 위치에 도달하는 경우의 수는 (파이프가 가로 방향인 상태에서 그대로 오른쪽으로 이동한 경우) + (파이프가 대각선 방향인 상태에서 가로 방향으로 전환하며 오른쪽으로 이동한 경우)가 된다.
- 파이프가 세로 방향인 상태로 특정 위치에 도달하는 경우의 수는 (파이프가 세로 방향인 상태에서 그대로 아래쪽으로 이동한 경우) + (파이프가 대각선 방향인 상태에서 세로 방향으로 전환하며 아래쪽으로 이동한 경우)가 된다.
- 파이프가 대각선 방향인 상태로 특정 위치에 도달하는 경우의 수는 (파이프가 가로 방향인 상태에서 대각선 방향으로 전환하며 오른쪽 아래로 이동한 경우) + (파이프가 세로 방향인 상태에서 대각선 방향으로 전환하며 오른쪽 아래로 이동한 경우) + (파이프가 대각선 방향인 상태에서 그대로 오른쪽 아래로 이동한 경우)가 된다.
- 위와 같은 개념을 사용하기 위해서는 각 방향으로 특정 위치에 도달하는 경우의 수를 저장하기 위한 3차원 배열을 만들어주어야 한다.
- dp[z][y][x]
- 이때 z는 파이프의 방향을 의미하며, y와 x는 각각 특정 위치의 행과 열을 의미한다.
- z = 0(가로) or 1(세로) or 2(대각선)
- 즉, dp[2][3][3]은 파이프가 대각선 방향인 상태로 (3, 3)의 위치에 도착하는 경우의 수를 의미한다.
💻 소스코드
DFS로 구현한 코드(Python3로 제출 시 시간초과 발생)
import sys
input = sys.stdin.readline
def dfs(y, x, state):
global cnt
if (y, x) == (n - 1, n - 1):
cnt += 1
return
if state == 0:
if x + 1 < n and house[y][x + 1] == 0:
dfs(y, x + 1, 0)
elif state == 1:
if y + 1 < n and house[y + 1][x] == 0:
dfs(y + 1, x, 1)
else:
if x + 1 < n and house[y][x + 1] == 0:
dfs(y, x + 1, 0)
if y + 1 < n and house[y + 1][x] == 0:
dfs(y + 1, x, 1)
if y + 1 < n and x + 1 < n:
if (house[y][x + 1], house[y + 1][x], house[y + 1][x + 1]) == (0, 0, 0):
dfs(y + 1, x + 1, 2)
n = int(input())
house = [list(map(int, input().split())) for _ in range(n)]
cnt = 0
dfs(0, 1, 0)
print(cnt)
DP 배열을 이용한 풀이
import sys
input = sys.stdin.readline
n = int(input())
house = [list(map(int, input().split())) for _ in range(n)]
# 0: 가로, 1: 세로, 2: 대각선
dp = [[[0] * n for _ in range(n)] for _ in range(3)]
# 파이프 시작 위치 및 방향 설정
dp[0][0][1] = 1
# DP를 수행하면서 현재 행의 윗 행을 사용해야하므로 첫 행을 먼저 초기화
for i in range(2, n):
if house[0][i] == 0:
dp[0][0][i] = dp[0][0][i - 1]
for y in range(1, n):
for x in range(2, n):
# 대각선 방향인 상태로 현재 위치에 올 수 있는 경우의 수
if (house[y][x], house[y - 1][x], house[y][x - 1]) == (0, 0, 0):
dp[2][y][x] = dp[0][y - 1][x - 1] + dp[1][y - 1][x - 1] + dp[2][y - 1][x - 1]
# 가로 또는 세로 방향인 상태로 현재 위치에 올 수 있는 경우의 수
if house[y][x] == 0:
dp[0][y][x] = dp[0][y][x - 1] + dp[2][y][x - 1]
dp[1][y][x] = dp[1][y - 1][x] + dp[2][y - 1][x]
# 파이프를 맵 끝으로 이동시키는 경우의 수는
# 각 방향인 상태로 맵 끝에 올 수 있는 경우의 수를 모두 더한 것과 같음
print(dp[0][n - 1][n - 1] + dp[1][n - 1][n - 1] + dp[2][n - 1][n - 1])'🥇 Problem Solving > Dynamic Programming' 카테고리의 다른 글
| [Python] BOJ / 14501번 / 퇴사 (0) | 2023.04.15 |
|---|---|
| [Python] BOJ / 2156번 / 포도주 시식 (1) | 2023.04.14 |
| [Python] BOJ / 2225번 / 합분해 (0) | 2023.04.12 |
| [Python] BOJ / 2133번 / 타일 채우기 (0) | 2023.04.12 |
| [Python] BOJ / 2096번/ 내려가기 (0) | 2022.06.30 |