1520번: 내리막 길
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으
www.acmicpc.net
문제
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으며, 각 지점 사이의 이동은 지도에서 상하좌우 이웃한 곳끼리만 가능하다.
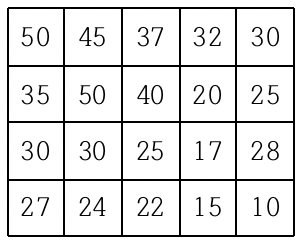
현재 제일 왼쪽 위 칸이 나타내는 지점에 있는 세준이는 제일 오른쪽 아래 칸이 나타내는 지점으로 가려고 한다. 그런데 가능한 힘을 적게 들이고 싶어 항상 높이가 더 낮은 지점으로만 이동하여 목표 지점까지 가고자 한다. 위와 같은 지도에서는 다음과 같은 세 가지 경로가 가능하다.



지도가 주어질 때 이와 같이 제일 왼쪽 위 지점에서 출발하여 제일 오른쪽 아래 지점까지 항상 내리막길로만 이동하는 경로의 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 지도의 세로의 크기 M과 가로의 크기 N이 빈칸을 사이에 두고 주어진다. 이어 다음 M개 줄에 걸쳐 한 줄에 N개씩 위에서부터 차례로 각 지점의 높이가 빈 칸을 사이에 두고 주어진다. M과 N은 각각 500이하의 자연수이고, 각 지점의 높이는 10000이하의 자연수이다.
출력
첫째 줄에 이동 가능한 경로의 수 H를 출력한다. 모든 입력에 대하여 H는 10억 이하의 음이 아닌 정수이다.
풀이
- 기본적으로는 경로 탐색 알고리즘을 사용한다.
- 다만 단순히 DFS만을 사용하여 문제를 풀 경우 시간 초과가 발생하기 때문에 이를 해결하기 위한 최적화 알고리즘이 필요하다.
- 문제에 드러난 예시를 잘 살펴보면 중복되는 경로를 탐색하는 경우가 발생하는 것을 확인할 수 있다.
- 생각해보면 만약 이미 특정 위치를 지나쳐서 목적지까지 가는 경우의 수를 알고있다면 즉, 이미 해당 위치를 방문하여 탐색을 수행하였다면 더 이상 탐색을 진행하지 않고도 목적지까지 가는 경우의 수를 갱신할 수 있다는 것이다.
- 이를 위해서 DP 배열을 사용하였으며, 자세한 설명은 아래 코드의 주석과 같다.
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10 ** 6)
dy = [0, 1, 0, -1]
dx = [1, 0, -1, 0]
def dfs(y, x):
# 목적지에 도착한 경우
if (y, x) == (m - 1, n - 1):
return 1 # 1을 리턴하여 DP 배열을 채워줌
# 현재 위치한 경로가 방문한 적이 없는 경로인 경우 네 방향에 대하여 탐색 수행
if dp[y][x] == -1:
dp[y][x] = 0 # 방문 여부 기록
for i in range(4):
ny = y + dy[i]
nx = x + dx[i]
if 0 <= ny < m and 0 <= nx < n:
if graph[ny][nx] < graph[y][x]:
dp[y][x] += dfs(ny, nx) # 새로운 경로를 찾음에 따라 DP 배열을 갱신
# 현재 위치한 경로에 이미 방문한 적이 있거나, 탐색이 끝난 경우
# 해당 위치에서 출발하여 목적지까지 가는 경로의 수를 리턴
return dp[y][x]
m, n = map(int, input().split())
graph = [list(map(int, input().split())) for _ in range(m)]
dp = [[-1] * n for _ in range(m)]
print(dfs(0, 0))'🥇 Problem Solving > Depth-First Search' 카테고리의 다른 글
| [Python] BOJ / 2573번 / 빙산 (0) | 2022.05.01 |
|---|---|
| [Python] BOJ / 1707번 / 이분 그래프 (0) | 2022.05.01 |
| [Python] BOJ / 1987번 / 알파벳 (0) | 2022.04.05 |
| [Python] BOJ / 10026번 / 적록색약 (0) | 2022.04.05 |
| [C++] BOJ / 1987번 / 알파벳 (0) | 2021.12.11 |